Performance at Scale¶
Sorted Containers scales extremely well. This page discusses why both in theory and in practice. The design of Sorted Containers permits testing through tens of billions of items and benchmarks present results at this scale. The results of this page would be difficult and expensive to replicate with other implementations.
Two methods are most important for analysis. Each stresses editing while
maintaining sorted order. The first is SortedList.add() which identifies
the insertion position using binary search. The second is
SortedList.__delitem__() which identifies the deletion position using
indexing. Most other methods are either symmetric or a subset of the runtime
complexity of these methods.
To fully grasp the content below, its strongly recommended that you read the implementation details first. Sorted Containers maintains a B-tree-like data structure limited to two levels of nodes.
Theory¶
To discuss the runtime complexity of Sorted Containers, we must consider two values:
n – the size of the sorted list.
m – the “load” or sublist length.
In a Sorted List with n elements, there will be a top-level list of
pointers to 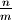 sublists each of which are approximately m
elements long. There will also be a “maxes” index which is the max of each
sublist. The index will contain
sublists each of which are approximately m
elements long. There will also be a “maxes” index which is the max of each
sublist. The index will contain 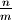 references.
references.
Now adding an element using SortedList.add() requires these steps:
Bisect the “maxes” index to find the appropriate sublist –
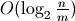
Bisect the sublist to find the appropriate insertion position –
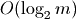
Insert the element in the sublist –
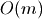
A sublist may be split and inserted into the top-level list –
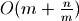
Consider how often step #4 may occur if we begin with a Sorted List of
n elements and add n more elements. The top-level list length will grow
from 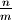 to
to 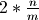 meaning that step #4 was
executed
meaning that step #4 was
executed 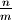 times.
times.
Altogether, growing a Sorted List of n elements by n more elements has the time complexity:
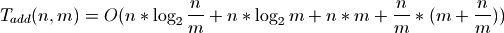
Now consider an extreme case:
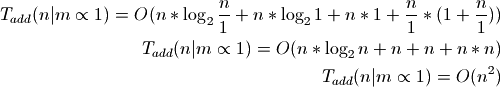
The above is why some consider Sorted Containers unscalable. Because the load is not chosen dynamically, in theoretical analysis, it must be treated as a constant with respect to n which makes it proportional to 1.
In practice, the default load is 1,000 which is generally closer to the square root or cube root of n. Consider where m is proportional to the square root of n:
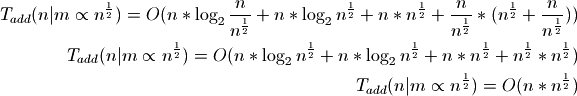
The amortized cost of adding an individual item is therefore proportional to the square root of n.
Our best bounds will be to use the cube root of n:
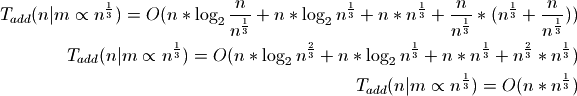
Now the amortized cost of adding an individual item is proportional to the cube root of n.
Alternative tree-based implementations have a runtime complexity proportional
to 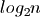 for adding elements. The logarithm grows much more slowly
than the cube root for large values of n. However, in practice we never reach
those large values and the constant factors involved have a significant
impact. Consider a billion elements:
for adding elements. The logarithm grows much more slowly
than the cube root for large values of n. However, in practice we never reach
those large values and the constant factors involved have a significant
impact. Consider a billion elements:
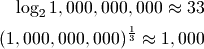
The constant factor between those is 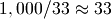 . So if the
operations for tree-based implementations are more than 33 times slower, then
Sorted Containers may be faster. Below I’ll make an argument for
why that occurs in practice.
. So if the
operations for tree-based implementations are more than 33 times slower, then
Sorted Containers may be faster. Below I’ll make an argument for
why that occurs in practice.
Now deleting an element using SortedList.__delitem__() requires these
steps:
Build the index if not present –
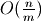
Traverse the index to resolve the internal location –
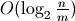
Delete the element in the sublist –
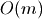
Update the index –
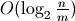
A sublist may be combined with a neighboring sublist if it becomes too small. When this happens, the index is deleted –
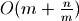
Consider how often steps #1 and #5 may occur if we begin with a
Sorted List of n elements and delete all n elements. The top-level
list will shrink from 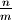 to zero meaning that steps #1 and #5
were executed
to zero meaning that steps #1 and #5
were executed 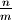 times.
times.
Altogether, deleting n elements from a Sorted List of n elements has the time complexity:
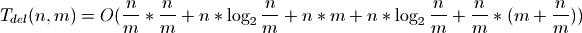
Most terms are the same for adding and deleting elements. But the first term is different. Rebuilding the index takes:
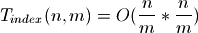
Furthermore index lookups and updates are proportional to 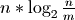 . All these terms are minimized with
. All these terms are minimized with 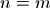 . However
that maximizes the cost of step (3),
. However
that maximizes the cost of step (3), 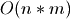 .
.
Once again our best bounds will be to use the cube root of n:
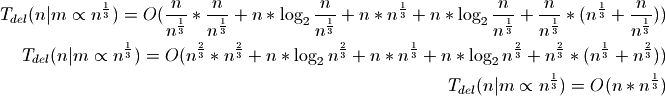
When deleting elements by index, the amortized time complexity is proportional to the cube root of n.
Although using ![m \propto \sqrt[3]{n}](_images/math/1b4e89aaa58410b8b2f9853b2f701c591dcfb42b.png) is the best theoretical time
complexity, index lookups, updates, and building are composed of expensive
operations. In practice, the square root of n works better when doing a lot
of numerical indexing.
is the best theoretical time
complexity, index lookups, updates, and building are composed of expensive
operations. In practice, the square root of n works better when doing a lot
of numerical indexing.
Python Implementations¶
I’ve now said that some operations are more expensive than others while still
considering each to take 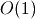 time. To understand this, we have to look
at how Python is implemented.
time. To understand this, we have to look
at how Python is implemented.
The most popular implementation of Python is CPython. CPython implements lists as arrays of pointers and integers as allocated memory objects. This means that shifting elements in lists is very fast. It’s akin to a mem-move operation for which modern processors are well optimized. The memory access pattern is entirely sequential.
In 64-bit builds of CPython, integers require approximately thirty bytes
each. This severely limits the number of integers we can hold in memory. In
2016, the largest commercial servers support up to terabytes of memory which
can hold only hundreds of billions of integers. While large in practice, the
number is small in theory. Doing integer math in CPython requires a memory
allocation which, while still 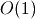 , is quite a bit more costly than a
processor-supported integer.
, is quite a bit more costly than a
processor-supported integer.
An optimized implementation of Python is PyPy. PyPy improves on CPython in many ways but one of the most important to our discussion is the use of “tagged pointers.” Tagged pointers are capable of storing integers within the pointer itself. This greatly reduces memory consumption so that many integers in PyPy take only eight bytes.
Lists of integers in PyPy are therefore packed densely together. When storing integers in a sorted list, both the “maxes” index and positional index are densely packed lists of integers. This improves locality for various processor cache features.
The access pattern of both indexes is also optimized for modern processors. Traversing both the “maxes” index and the sublist uses bisect which while initially random, narrows locality with each iteration. Likewise the positional index is a tree, densely stored in a list. The memory access pattern locality is very good initially and then becomes random, the exact opposite of bisect.
The benchmarks below use PyPy, without loss of generality, to maximize memory utilization and performance.
Sampling¶
As described in the theory section above, some costs in sorted lists are amortized over many operations. Amortized algorithms present unique difficulties in measuring performance as, by design, expensive operations are avoided.
For example, consider measuring the expected value of the lottery without knowing the total jackpot. Purchasing a thousand tickets may still result in no winnings which would conclude incorrectly an expected value of zero.
More practically, consider the list data type in CPython. Lists grow and shrink as necessary but the underlying implementation is restricted to static allocations. For this reason, lists are often over-allocated so that most appends may occur immediately. Occasionally, the list must be reallocated and possibly copied, which takes linear time. If we sampled performance by initializing lists of various sizes and appending an element, we may never observe a resize operation and so over-estimate performance.
One solution for both Python lists and Sorted Containers sorted lists would be to double the size or remove all elements from the initialized list as was done in the Theory section above. Unfortunately, that method is too expensive to be practical. Doing so would require weeks and months of time incurring hundreds and thousands of dollars in machine costs.
To shorten the measured time, two techniques are used. The first constructs sorted lists very quickly by initializing private member variables directly. The latter uses sampling in representative scenarios to perform a hundredth of the operations needed to double the size or remove all elements.
The problem solved here is similar to that faced by binary tree
implementations, like red-black trees, which do not maintain a binary tree in
perfect balance. In fact, the maximum height of a red-black tree is 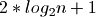 . While still
. While still 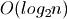 , the constant factor can have a
big impact on performance analysis. When using sampling to measure the
performance of red-black trees, trees of various shapes and heights must be
used. The same is done here with Sorted Containers.
, the constant factor can have a
big impact on performance analysis. When using sampling to measure the
performance of red-black trees, trees of various shapes and heights must be
used. The same is done here with Sorted Containers.
Consider a sorted list initialized from an iterable of random values. Those values are sorted using the “sorted” builtin function and the resulting list is chopped into sublists of the given load. The “maxes” index is simply the last element of each sublist. If we plotted sublist length as a histogram, there would be one tall bar at the load size. In this scenario, all sublists are the same length which works very well in practice but is misleading for sampling performance.
To more accurately measure performance, we must consider sublist lengths as random values are added individually. The video below displays a histogram of sublist lengths as random values are added to a sorted list. The load is one thousand.
The histogram of sublist lengths is in blue while a normal curve fitted to the histogram is plotted in green. The size of the sorted list grows to millions of elements. Notice the fit of the normal curve improves with time. The sublist lengths grow from one to two thousand elements, at which point sublists are split and the process repeats. At the boundaries, bimodal distributions occur which may be approximated as a normal distribution that wraps-around at the limits.
Consider also a sorted list with a million values each of which is removed at random. The video below displays a histogram of sublist lengths as values are random deleted from the sorted list. The load is again one thousand.
The sorted list was initialized with a million values. Notice all sublists begin with the same length represented by a spike in the histogram. As elements are deleted, the spike moves toward five hundred. When sublists become too small they are combined with neighboring sublists. Those neighboring sublists may be any size between 500 and 2,000. This behavior results in new peaks at 1,000, 1,500, and 2,000. Each of those peaks then begins traversing left and the process repeats. The overall effect is like watching ripples. Over time each ripple starts as a sharp-looking normal curve and then flattens out.
In modeling each of the above cases, a normal curve is used to represent the
sublist lengths. When adding elements, the range of the curve is bounded by
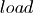 and
and 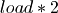 . While deleting elements the curve is bounded
by
. While deleting elements the curve is bounded
by 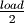 and
and 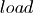 . The curve wraps-around these
limits. Normal distributions have two parameters:
. The curve wraps-around these
limits. Normal distributions have two parameters: 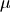 and
and
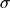 which are the mean and standard deviation. Several means are
tested to improve sampling, each called a “moment.” When adding elements, there
are ten moments evenly distributed in the range. And when deleting elements,
there are five moments evenly distributed in the range. The parameter,
which are the mean and standard deviation. Several means are
tested to improve sampling, each called a “moment.” When adding elements, there
are ten moments evenly distributed in the range. And when deleting elements,
there are five moments evenly distributed in the range. The parameter,
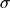 , is given as a tenth of the load,
, is given as a tenth of the load, 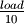 .
.
With this information about the distribution of sublist lengths, we can very quickly construct large sorted lists. To do so, we sample lengths from a normal distribution and construct the sublists from sequential integers up to the desired size. The “maxes” index is simply given as the last element in each sublist. Because sequential integers are used, sublists are already sorted.
After constructing a sorted list at each of the moments in the sublist length range, operations are performed to total a hundredth of the total size. The total time is the sum of the time at each moment. This process is repeated five times and the median is selected from the measurements. The median is often more accurate than the minimum due to cache effects. Details of the memory cache hierarchy are described below.
Benchmarks¶
Two benchmarks are measured. The first is adding random values to a sorted list and the second is deleting random indices from a sorted list. When adding values, the load is set to the cube root of the list size. And when deleting random indices, the load is set to the square root of the list size.
Each table below displays: the method used, the initial size of the sorted list, the number of operations performed, the sum of the times at each moment as the total time, the operations completed per second, and the ratio of the previous Ops/Sec to the current Ops/Sec.
In theory, using a load equal to the cube root of the list size should yield an
algorithmic time complexity of ![n * \sqrt[3]{n}](_images/math/d418f23efcc1a5845e2afdcaaa74b120a9e00c20.png) . With a bit of math, we
can calculate the expected Ops/Sec ratio as 2.154. Similarly, with a load equal
to the square root of the list size, the time complexity should be
. With a bit of math, we
can calculate the expected Ops/Sec ratio as 2.154. Similarly, with a load equal
to the square root of the list size, the time complexity should be 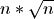 . In that scenario, the Ops/Sec ratio should be 3.162.
. In that scenario, the Ops/Sec ratio should be 3.162.
Tree-based sorted list implementations often advertise 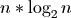 time complexity for which, at extremely large sizes, the Ops/Sec ratio would
approach one. However, at the sizes discussed below, the ratio is closer to
1.136. This means that as we grow from one million to one billion elements, we
expect a net ratio of ~2. By comparison, the cubic root time complexity would
expect a net ratio of ~10. In practice, Sorted Containers is
often five to ten times faster at smaller list sizes. So the total effect is
for performance to be equal at large list sizes. Also, tree-based
implementations have difficulty trying to realize the theoretical ratio and so
remain slower even at scale.
time complexity for which, at extremely large sizes, the Ops/Sec ratio would
approach one. However, at the sizes discussed below, the ratio is closer to
1.136. This means that as we grow from one million to one billion elements, we
expect a net ratio of ~2. By comparison, the cubic root time complexity would
expect a net ratio of ~10. In practice, Sorted Containers is
often five to ten times faster at smaller list sizes. So the total effect is
for performance to be equal at large list sizes. Also, tree-based
implementations have difficulty trying to realize the theoretical ratio and so
remain slower even at scale.
Local Results¶
Measurements were made locally on a MacBook Pro (Retina, Late 2013) with 2.6 GHz Intel Core i7 processor and 16 GB of 1,600 MHz DDR3 memory. Sorted list sizes ranged from one million to one billion elements. The benchmark required approximately twelve gigabytes of memory.
Method |
Size |
Operations |
Time |
Ops/Sec |
Ratio |
|---|---|---|---|---|---|
add |
1e+06 |
1e+04 |
0.01501 |
666045.025 |
nan |
add |
1e+07 |
1e+05 |
0.26612 |
375764.681 |
1.773 |
add |
1e+08 |
1e+06 |
4.69080 |
213183.298 |
1.763 |
add |
1e+09 |
1e+07 |
83.01831 |
120455.358 |
1.770 |
The above table displays the performance of adding elements to a sorted list. Notice the particularly good ratio, approximately 1.77, out-performed the theoretically expected 2.154. This is mainly due to the different constant times required for various operations, of which memory plays a large role and is discussed below.
Method |
Size |
Operations |
Time |
Ops/Sec |
Ratio |
|---|---|---|---|---|---|
del |
1e+06 |
1e+04 |
0.00827 |
1208897.485 |
nan |
del |
1e+07 |
1e+05 |
0.13309 |
751393.836 |
1.609 |
del |
1e+08 |
1e+06 |
3.79143 |
263752.866 |
2.849 |
del |
1e+09 |
1e+07 |
124.59184 |
80262.081 |
3.286 |
When deleting elements, the ratio starts by out-performing the theoretically expected 3.162 but increases with size. The limited processor caches at these large sizes play a significant role in the performance. Traversing the positional index will evict elements of the top-level list and sublists.
Virtual Machine Results¶
Virtual machine results were made on a Google Compute Engine, Haswell generation, 2.3 GHZ Intel Xeon processor with 208 GB of memory. Sorted list sizes ranged from one million to ten billion elements. The benchmark required approximately 128 gigabytes of memory.
Method |
Size |
Ops |
Time |
Ops/Sec |
Ratio |
|---|---|---|---|---|---|
add |
1e+06 |
1e+04 |
0.02133 |
468884.826 |
nan |
add |
1e+07 |
1e+05 |
0.38629 |
258872.924 |
1.811 |
add |
1e+08 |
1e+06 |
6.20695 |
161109.825 |
1.607 |
add |
1e+09 |
1e+07 |
120.24735 |
83161.919 |
1.937 |
add |
1e+10 |
1e+08 |
2416.60713 |
41380.330 |
2.010 |
As with local results, the ratio out-performed the theoretically expected 2.154 at small list sizes. At very large sizes processor caches played more significant roles and the ratio approached the theoretically expected value.
Method |
Size |
Ops |
Time |
Ops/Sec |
Ratio |
|---|---|---|---|---|---|
del |
1e+06 |
1e+04 |
0.01791 |
558289.343 |
nan |
del |
1e+07 |
1e+05 |
0.26171 |
382097.449 |
1.461 |
del |
1e+08 |
1e+06 |
6.11150 |
163626.036 |
2.335 |
del |
1e+09 |
1e+07 |
171.58899 |
58278.798 |
2.808 |
del |
1e+10 |
1e+08 |
5493.95076 |
18201.838 |
3.202 |
The virtual machine results are again similar to local measurements. At smaller list sizes the ratio out-performs the expected 3.162 but increases at larger sizes.
Total cost of the rented virtual machine was $33.97 for 1,011 minutes of use. Anyone interested in funding further scaling to one hundred billion elements should contact the project lead.
Memory¶
Modern processors use multiple caches to improve memory performance. Caches are organized into individual levels: L1, L2, and L3. Each successive level is larger and slower than the previous level. For example, the size and average latency for random memory accesses on Intel’s latest Skylake i7-6700 processor:
L1 Cache, 64 KB, ~4 cycles
L2 Cache, 256 KB, ~12 cycles
L3 Cache, 8 MB, ~42 cycles
RAM, 16 GB, ~446 cycles
The exact size and latency are not important but the ratios are significant. L2 cache is about four times larger and slower than L1 cache. L3 cache is thirty times larger and four times slower than L2 cache. And memory is two thousand times larger and ten times slower than L3 cache. These ratios are approximate but illustrative of the slowdowns.
Also important is the memory access pattern. These advertised latencies are averages for random memory access. But there are two other patterns often seen in practice: sequential and data-dependent.
Sequential memory access is faster than random due to its predictable nature. The speedup varies but about five times faster is a reasonable guess. Striding through memory sequentially will incur almost zero cycle stalls.
Data-dependent memory access is slower than random because no parallelization can occur. Each successive memory access depends on the previous and so stalls the processor. The pattern is typical of dereferencing pointers. Again its difficult to quantify the slowdown but five times slower is a reasonable guess. Altogether, jumping around memory with data-dependent accesses could be one thousand times slower than sequential accesses.
Given the size and latencies for memory in modern processors, consider the typical cost of adding an element to a sorted list with size one billion. First the “maxes” index will be bisected. The index will be one million integers densely packed in a list. Using PyPy, the entire index could fit in the L3 cache. As the list is bisected, nearby indexes will be pulled into the L2 and L1 cache and lookups will accelerate a hundred times. Once the sublist is found, it too will be bisected. The sublist will contain only one thousand integers and those too will be quickly pulled from memory into L3, L2, and L1 caches. Once bisected, the new value will be inserted and memory will be traversed sequentially to make space.
For comparison, consider traversing an AVL-binary tree with one billion elements. A highly optimized implementation will require at least 24 gigabytes of memory. The binary tree will likely traverse thirty levels, each of which is a data-dependent lookup. Some lookups will have good locality but most will not. Each lookup could be hundreds to thousands of times slower than sequential accesses. These slow lookups are why Sorted Containers can afford to shift a thousand sequential elements in memory and have most additions take less time than binary tree implementations.
Due to the memory cache hierarchy, Sorted Containers scales extremely well. Each element in a Sorted List has little overhead which increases cache utilization. Data is randomly accessed and related data is stored together. These patterns in computing have held for decades which promises Sorted Containers a bright future.
